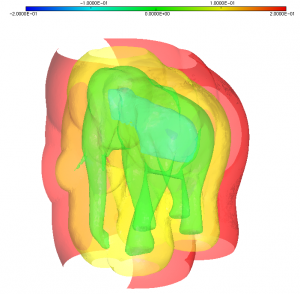
The mmg3d application allows to discretize and optimize an implicitly defined surface (which mean a surface defined by a level-set function). You can find more informations about the used algorithm here.
Note that this page contains only few examples of isosurface discretization. As mmg2d and mmg3d have lot of options in common, you can refer to the 2d examples for:
- example of isosurface discretization with mesh adaptation;
- example of input materials preservation (multi-material mode);
- example of bubble removal (small parasitic component deletion).
Example
We start from the cube.mesh cube mesh and the discrete level-set function at the mesh nodes (elephant.sol file) displayed figure 1.
Figure 1: Iso surfaces of the level-set function defined at the nodes of the cube mesh
To split the domain on the 0 value of the level-set function:
mmg3d_O3 cube -sol elephant.sol -ls -nr -hausd 0.001 -hgrad 1.3 -hmax 0.05
- As previously, we specify the name of the .sol file, that contains here the level-set function values at mesh nodes, using the -sol option (more infos about the -sol option).
- The -ls option states that the input .sol file is in fact a level-set file and that we want to discretize the implicit surface defined by the 0 level of the level-set.
- A level-set function is a smooth function, thus we don’t want to detect ridges and we use the -nr option;
- The cube mesh bounding box size is of [1 x 1 x 1] thus a hausdorff parameter (-hausd option) of 0.001 allows to have a good surface approximation (more infos about the -hausd option).
- We increase the authorized ratio between consecutive edges using the -hgrad option (more infos about the -hgrad option).
- Last, the -hmax option ensure that we do not create edges longer than 0.05 (more infos about the -hmax option).
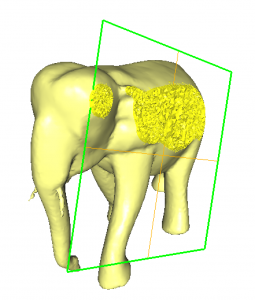
We obtain two domains separated by a surface that is an optimized mesh of the initial implicit surface (see figure 2).
Note that Mmg impose the reference (=color) of the isosurface and of the domains :
- The isosurface is created with the ref 10;
- The volume inside the iso surface has the ref 3;
- The volume outside the ref 2.
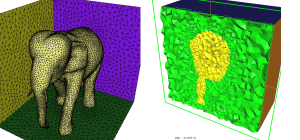
Figure 2: Final cube mesh: Implicit surface mesh (left) and cut through the volume cube mesh (right)
Preservation of one given subdomain and analysis mode
Mmg allows to save a given subdomain of a mesh containing multiple subdomains using the -nsd option. You can for example run Mmg on your output mesh (cube.o.mesh file) save only the elephant mesh (domain of reference 3) with the following command line:
mmg3d_O3 cube.o.mesh -noinsert -noswap -nomove -nsd 3
Figure 3: Saving of only the subdomain of reference 3 using the -nsd option
The coupling of the -noinsert, -noswap and -nomove options forbid all the Mmg operators, thus the cube.o.mesh mesh is analyzed but not remeshed.
Level-set discretization with input domains preservation (multi-material mode) and small parasitic components removal
You can refers to the 2d example : https://www.mmgtools.org/mmg-remesher-try-mmg/mmg-remesher-tutorials/mmg-remesher-mmg2d/implicit-domain-meshing
Boundary level-set splitting
With -lssurf option, it is possible to split only domain boundaries along the level-set while not splitting the interior of the mesh. Starting from the peninsula.mesh mesh file, the ls.sol level-set file and the peninsula.mmg3d reference mapping (provided after command line), we run the following command:
mmgs_O3 -lssurf peninsula.meshcat > peninsula.mmg3d <<EOF
LSReferences
5
1 10 11
2 3 4
38 5 6
37 7 8
0 nosplit
EOF
we obtain the figure 4:
- Mesh boundaries are splitted if ask and are assigned the wanted references
- internal domains (tetra) are not
Figure 4: Boundaries splitting using lssurf option
Note that if a mapping is provided for one of the input boundary references, then the mapping for all boundary references has to be given too.
