We start from the hole.mesh mesh (see Figure 1).
Figure 1: Initial mesh (hole.mesh)
This mesh contains a hole and 2 domains with different references, the yellow domain and the pink one.
Default paramteters
To run Mmg2d, you only have to run the application followed by the mesh name:
mmg2d_O3 hole.mesh
We obtain an output file named hole.o.mesh (depicted Figure 2): Mmg tries to unrefine the mesh while preserving the maximal distance between the ideal geometry and its discretisation (-hausd parameter, 0.01 by default) and with respect to the prescribed gradation ( -hgrad option, 1.3 by default) that impose the maximal ratio between the lengths of two adjacent edges. You will find more informations about this options below.
Figure 2: Output mesh without parameters
Boundary approximation control
The boundary approximation is controlled by the Hausdorff parameter. You can use the -hausd option to adapt the Hausdorff value to your needs (more infos about the -hausd option). We obtain the result displayed Figure 3 by asking for a maximal Hausdorff distance of 0.1 (our mesh bounding box is [-5 ; 10]x[-5 ; 10] ):
mmg2d_O3 -hausd 0.1 hole.mesh
Figure 3: Output mesh for a hausdorff parameter of 0.1 (the square is [-5 ; 10]x[-5 ; 10])
Remarks:
- The Hausdorff parameter leads to refine the mesh in areas with high curvature;
- The Hausdorff parameter depends of your mesh/object sizes, thus, the default value will rarely fit your needs;
- Knowing the mesh bounding box is very useful to fit the Hausdorff parameter: you can get this bounding box when you visualize your mesh with Medit;
- The default value (0.01) suits for a circle with radius of 1.
Gradation
The -hgrad parameter control the mesh gradation (i.e. the ration between the lengths of two adjacent edges, more infos about the -hgrad option). By default this parameter is setted to 1.3. You can disable the gradation using the -hgrad -1 value or customize the ratio value using the -hgrad val option (see Figure 4). Note that disabling the gradation can lead to meshes with bad qualities.
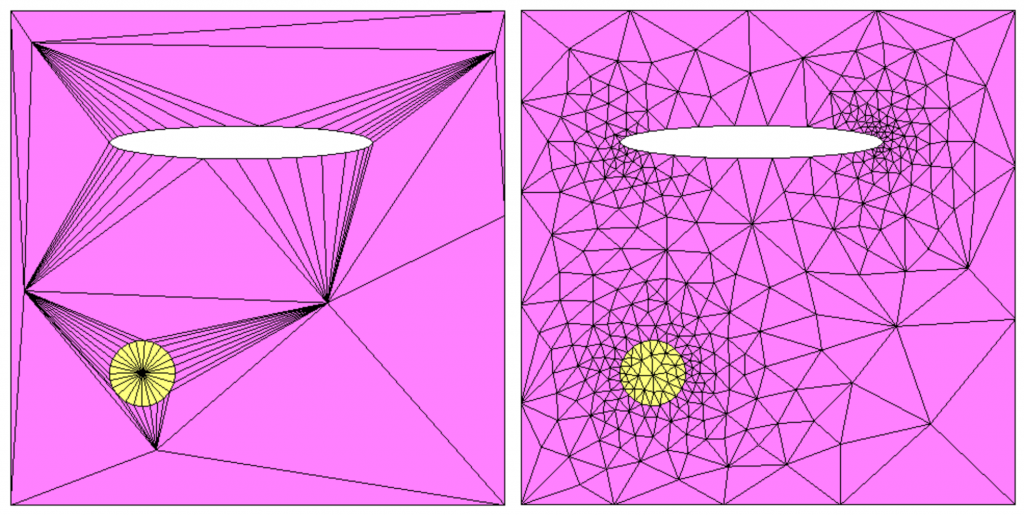
Figure 4: influence of the gradation parameter. Left, the gradation is disabled (-hgrad -1), right, it is setted to 2.3 (-hgrad 2.3)
Constant mesh size
You can prescribe a constant edge size using the -hsiz option:
mmg2d_O3 hole.mesh -hsiz 0.25
In this case, Mmg will create a mesh that will respect the intersection between the size map prescribed by the hausdorff parameter and the constant size map (which means that we keep the smallest size asked). This intersected size map still respects the gradation parameter (see Figure 5).
Figure 5: Output mesh when asking for a constant mesh size of size 0.25 (-hsiz 0.25)
Adaptation to an input size map
A size map can be supplied to mmg in order to impose a desired size feature when remeshing the input mesh (hole.mesh). This size map is a scalar / tensorial function defined at the mesh vertices. At each vertex, it associates the desired size of the surrounding elements of the mesh.
Size maps must be encoded in:
- a .sol file if you use input mesh at Medit file format. Mmg automatically detects and use a sol file with the same name than your input mesh file (hole.sol in our example), otherwise, you can specify another sol file using the -sol option (-sol mysolfile.sol)
- the NodeData field of your .msh file if you use Gmsh file format. In this case, the string tag of the NodeData field must contains the :metric keyword.
For example, the hole.sol file contains a scalar size map that asks for edges of length 0.1 at vertices with abscissa between 1 and 3 and of size 1 outside this area (see Figure 6, left). As the sol file has the same name than the mesh file, Mmg will automatically read it and the following command line will adapt the mesh to the wanted size map :
mmg2d_O3 hole.mesh
Figure 6: prescirbed size map (left) and adapted output mesh (right).
