The mmgs application allows to discretize and optimize an implicitly defined line (which means a line defined by a level-set function). It takes a 3D surface mesh (i.e. a set of triangles) and the values of the level-set function at the mesh nodes and returns another 3D surface mesh (that represents the same underlying geometry) with the explicit discretization of the wanted isovalue and the two new domains defined by this isovalue (conformingly connected).
Example
We start from the teapot.mesh mesh and the distance function to a cube discretized at the mesh nodes (cube-distance.sol file). The input mesh and the distance function are displayed figure 1.
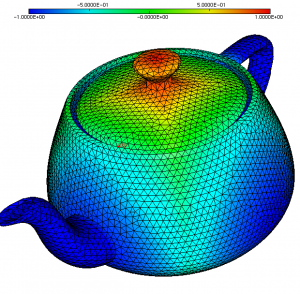
Figure 1: Surface mesh of a teapot (it contains only triangles, no tetrahedra) and distance function to a cube inscribed in the teapot.
To split the domain on the 0 value of the level-set function:
mmgs_O3 teapot -sol cube-distance.sol -ls
- we specify the name of the .sol file, that contains here the level-set function values at mesh nodes, using the -sol option (more infos about the -sol option).
- The -ls option states that the input .sol file is in fact a level-set file and that we want to discretize the implicit line defined by the 0 level of the level-set. You can specifiy another value than 0 by providing it as argument of the -ls argument.
We obtain two domains conformingly connected and separated by a line that is a discretization of the initial 0 level-set (see figure 2).
Note that by default Mmg imposes the reference (=color) of the isosurface and of the domains :
- The isoline is created with the ref 10;
- Triangles in the negative part of the distance function have the ref 3;
- Triangles in the positive part of the distance function have the ref 2.
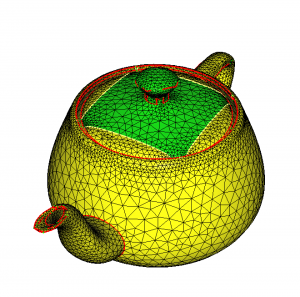
Figure 2: Final teapot mesh: the yellow line represents the isovalue 0 of the distance function, the green domain its positive part, the yellow one its negative part. Red lines are ridges added by the automatic sharp angle detection.
Preservation of input references (colors)
By default, Mmgs resets the references (colors) of the input mesh. In the previous example, the input teapot has multiple colors (see figure 3).
It is possible to ask Mmgs to preserve its:
mmgs_O3 teapot -sol cube-distance.sol -ls -keep-ref
The result is displayed figure 4.
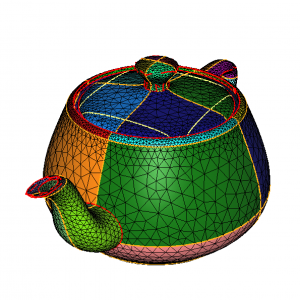
Figure 4: Output mesh after isovalue discretization with preservation of input references. The newly discretized isoline is still depicted in yellow.
Note that you can also preserve input references by the same way than in mmg2d and mmg3d, whith a parameter file. This last way is probably more robust and allow the removal of small parasitic components (-rmc option) and of implicit domains not connected to specific boundary conditions (LSBaseReference mode).
Example 4: Boundary level-set splitting
With -lssurf option, it is possible to split only domain boundaries (feature edges / lines here) along the level-set while not splitting the interior of the mesh (triangles). Starting from the peninsula.mesh mesh file and ls.sol level-set and the peninsula.mmgs reference mapping (provided after command line), we run the following command:
mmgs_O3 -lssurf peninsula.mesh
cat > peninsula.mmg3d <<EOF
LSReferences
5
1 10 11
2 3 4
38 5 6
37 7 8
0 nosplit
EOF
we obtain the figure 5:
- Mesh lines are splitted if ask and are assigned the wanted references
- internal domains (triangles) are not
- remark: on this test case, feature edges are marked as ridges by Mmg, thus, it is needed to remove the display of the ridges from the output medit file to see edge colors.
Note that if a mapping is provided for one of the input boundary references, then the mapping for all boundary references has to be given too.
Associated pages
Isovalue discretization algorithm, Documentation



