Mesh adaptation

This section describes the mesh adaptation process and the mesh modification operations related to it. The default version of the algorithm is performed by the following function:

int MMG5_mmg3d1_delone(MMG5_pMesh mesh, MMG5_pSol met, MMG5_int *permNodGlob)

Main adaptation routine.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• permNodGlob – if provided, strore the global permutation of nodes

Returns:

0 if failed, 1 if success.

The remeshing strategy in mmg3d relies on the intertwining of four local remeshing operations, namely:

• Edge split: a new vertex is created and inserted on long edges, which are then split into two smaller edges. The underlying tetrahedra are split and updated accordingly.

• Edge collapse: endpoints of a short edge are merged and the underlying tetrahedra are updated accordingly.

• Edge swap: positions of the vertices are unaltered, but the connections between tetrahedra are modified.

• Vertex relocation: one vertex is moved (and its connections are unaltered) with the aim to improve mesh quality.

Below is a general overview of the remeshing procedure in mmg3d. There are three main stages:

1. At first, function \(\texttt{MMG5_anatet}\) is called, with its parameter \(\texttt{typchk}\) set to 1. This implies that, throughout the call, edge length criteria are based on Hausdorff distance. The objective is to obtain a good sampling of the surface. This procedure encompasses a succession of (in this order):

   • Boundary edge splits, performed by calling the function \(\texttt{MMG3D_anatets}\),

   • Internal edge splits, performed by \(\texttt{MMG3D_anatetv}\) (pattern mode only),

   • Edge collapses, via function \(\texttt{MMG5_coltet}\),

   • Edge swaps, thanks to functions \(\texttt{MMG5_swpmsh}\) (for surface edge swaps) and \(\texttt{MMG5_swptet}\) (for internal edge swaps).

2. Then, a metric is defined, and graded, thanks to the functions \(\texttt{MMG3D_defsiz}\) and \(\texttt{MMG3D_gradsiz}\). The resulting \(\texttt{met}\) field is defined at the vertices of \(\texttt{mesh}\), and it contains the local size prescription at these entities.

   A second round of iterations of the function \(\texttt{MMG5_anatet}\) is carried out, with variable \(\texttt{typchk}\) set to 2. This indicates that the remeshing operators described above are triggered based on the local size prescribed by \(\texttt{met}\) (e.g. the notions of long and short edge).

3. Finally, one last round of iterations is carried out, using the function \(\texttt{MMG5_adptet_delone}\). Vertex relocations are introduced in this step for quality enhancement.

First adaptation step: surface sampling

The first step of mesh adaptation is performed by calling:

int MMG5_anatet(MMG5_pMesh mesh, MMG5_pSol met, int8_t typchk, int patternMode)

Analyze tetrahedra and split if needed.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• typchk – type of checking for edges length.

• patternMode – flag to say if we perform vertex insertion by patterns or by delaunay kernel.

Returns:

0 if fail, number of new points otherwise.

This function performs an iterative process of mesh adaptation. It stops after a set number of iterations or if no modifications have been made during one iteration. The content of an iteration starts with analysis and splitting of surface edges.

Edge split

Splitting operations are performed by different functions, depending on the parameters: in isotropic mode, splitting is performed by function

static MMG5_int MMG3D_anatets_iso(MMG5_pMesh mesh, MMG5_pSol met, int8_t typchk)

Analyze tetra and split on geometric criterion.

Remark

ridge points creation: with fem (finite element method) mode a tetra cannot have 2 boundary faces. Thus, the ridge point is created from a given tetra and it is seen a second time from another tetra, which allows to update its second normal. With nofem mode, a ref edge or ridge can be at the interface of 2 boundary faces belonging to the same tetra.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• typchk – type of checking permformed for edge length (hmax or MMG3D_LLONG criterion).

Returns:

-1 if failed.

Returns:

number of new points.

In anisotropic mode, it is done by:

static MMG5_int MMG3D_anatets_ani(MMG5_pMesh mesh, MMG5_pSol met, int8_t typchk)

Split surface edges on geometric criterion.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• typchk – type of checking permformed for edge length (hmax or MMG3D_LLONG criterion).

Returns:

-1 if failed.

Returns:

number of new points.

Both of these functions deal with splitting of surface tetrahedra. Additionally, in pattern mode, i.e. in the mode that uses pattern strategies to perform splittings (opposed to the default mode, which resorts to the Delaunay kernel), function \(\texttt{MMG3D_anatetv}\) is called as well, to deal with internal tetrahedra splits.

The process goes as follows:

1. First, a loop over all surface elements (identified by the existence of a \(\texttt{xtetra}\) field) is performed in order to review all surface edges. An edge may be too long regarding input max length or regarding Hausdorff distance. In both cases, edges that are considered too long are flagged for splitting. Then, the Bezier patch is computed on the current triangle. New points are then inserted according to the patch.

2. Then, flags are made consistant through the whole mesh: an flagged edge in a tetrahedron should be seen as flagged by all tetrahedra sharing this edge.

3. Splitting simulations are performed for all triangles containing at least one flagged edge. All splits leading to an invalid configuration are cancelled and the newly created points are deleted. In some cases, a dichotomy may be performed to find a valid configuration.

4. Finally, valid splits are actually performed via patterns.

Edge collapse

The second step of \(\texttt{MMG5_anatet}\) deals with edge collapse. The edge collapse operation is perhaps the most delicate one of the four. It operates on an edge \(\texttt{nump-numq}\) of the mesh, and merges \(\texttt{nump}\) onto \(\texttt{numq}\), as illustrated below in two dimensions. As a result:

• All the tetrahedra in the shell of \(\texttt{nump-numq}\) (i.e. those tetrahedra containing \(\texttt{nump}\) and \(\texttt{numq}\) as vertices) disappear.

• All the tetrahedra in the ball of \(\texttt{nump}\), and not in the shell of \(\texttt{nump-numq}\) (i.e. those tetrahedra containing \(\texttt{nump}\) but not \(\texttt{numq}\) as vertex) have \(\texttt{nump}\) replaced by \(\texttt{numq}\).

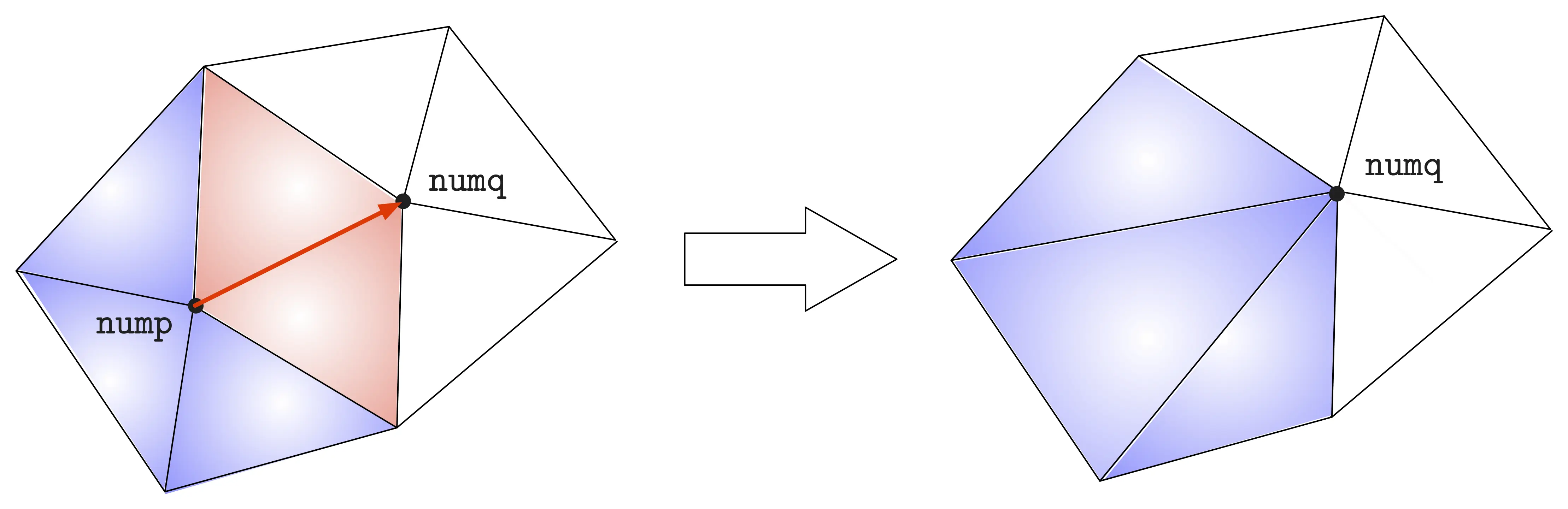
In two space dimensions, collapse of point \(\texttt{nump}\) onto \(\texttt{numq}\): the red elements in the shell of \(\texttt{nump-numq}\) disappear, and the vertex \(\texttt{nump}\) is replaced by \(\texttt{numq}\) in the elements in the ball of \(\texttt{nump}\).

All edges of the mesh are travelled and analyzed to see if collapse is suitable, using function:

static MMG5_int MMG5_coltet(MMG5_pMesh mesh, MMG5_pSol met, int8_t typchk)

Attempt to collapse short edges.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• typchk – type of edge length criterion (hmin or LSHORT criterion).

Returns:

negative value in case of failure, number of collapsed points otherwise.

Again, two modes are available, depending on whether \(\texttt{typchk}\) equals 1 (in which case, short edges are identified according to their length with respect to the input parameter \(\texttt{hmin}\)) or 2 (when the length is calculated with respect to the size prescriptions in \(\texttt{met}\)). During the first call to \(\texttt{MMG5_anatet}\), \(\texttt{typchk}\) is set to 1.

Several checks are in order when it comes to collapsing one point onto another. Once an edge (identified by a tetrahedron \(\texttt{k}\), a face \(\texttt{iface=0,1,2,3}\) in \(\texttt{k}\) and an edge \(\texttt{iedg=0,1,2}\) on this face) has been flagged as too short, the remainder of the process depends on the geometrical configuration. First, information about the surrounding elements should be computed. If the edge does not belong to a boundary face, the volumic ball of point \(\texttt{nump}\) is computed by:

int MMG5_boulevolp(MMG5_pMesh mesh, MMG5_int start, int ip, int64_t *list)

Given a vertex and a tetrahedron, find all tetrahedra in the ball of this vertex.

Fill the volumic ball (i.e. filled with tetrahedra) of point ip in tetra start. Results are stored in the form \(4*kel + jel\), kel = number of tetrahedra, jel = local index of p within kel.

Parameters:

• mesh – pointer to the mesh structure.

• start – index of the starting tetrahedra.

• ip – local index of the point in the tetrahedra start.

• list – pointer to the list of the tetra in the volumic ball of ip.

Returns:

0 if fail and the number of the tetra in the ball otherwise.

If the edge belongs to a boundary face, and if the edge is manifold, both volumic and surfacic balls must be computed, by calling:

int MMG5_boulesurfvolp(MMG5_pMesh mesh, MMG5_int start, int ip, int iface, int64_t *listv, int *ilistv, MMG5_int *lists, int *ilists, int isnm)

Compute the volumic ball of a SURFACE point p, as well as its surfacic ball, starting from tetra start, with point ip, and face if in tetra volumic ball:

• listv[k] = 4* tet index + index of point surfacic ball.

• lists[k] = 4* tet index + index of boundary face.

Warning

Don’t work for a non-manifold point if start has an adjacent through iface (for example : a non-manifold subdomain). Thus, if ip is non-manifold, must be called only if start has no adjacent through iface.

Parameters:

• mesh – pointer to the mesh structure.

• start – index of the starting tetra.

• ip – index in start of the looked point.

• iface – index in start of the starting face.

• listv – pointer to the computed volumic ball.

• ilistv – pointer to the computed volumic ball size.

• lists – pointer to the computed surfacic ball.

• ilists – pointer to the computed surfacic ball size.

• isnm – 1 if ip is non-manifold, 0 otherwise.

Returns:

-1 if fail, 1 otherwise.

If the edge belongs to a boundary face and it is not manifold (identified by tag \(\texttt{MG_NOM}\)), two cases arise. If the point is internal, the same function as standard internal points, \(\texttt{MMG5_boulevolp}\), is used. If the point is not internal, surfacic and volumics balls for these types of points are computed by:

int MMG5_boulesurfvolpNom(MMG5_pMesh mesh, MMG5_int start, int ip, int iface, int64_t *listv, int *ilistv, MMG5_int *lists, int *ilists, MMG5_int *refmin, MMG5_int *refplus, int isnm)

Compute the volumic ball of a SURFACE point p, as well as its surfacic ball, starting from tetra start, with point ip, and face if in the volumic ball. listv[k] = 4*number of tet + index of point surfacic ball. lists[k] = 4*number of tet + index of face.

Warning

Doesn’t work for a non-manifold point if start has an adjacent through iface (for example: a non-manifold subdomain). Thus, if ip is non-manifold, must be called only if start has no adjacent through iface.

Parameters:

• mesh – pointer to the mesh structure.

• start – index of the starting tetrahedron.

• ip – index in start of the desired vertex.

• iface – index in start of the starting face.

• listv – pointer to the computed volumic ball.

• ilistv – pointer to the computed volumic ball size.

• lists – pointer to the computed surfacic ball.

• ilists – pointer to the computed surfacic ball size.

• refmin – return the reference of one of the two subdomains in presence

• refplus – return the reference of the other subdomain in presence

• isnm – is the vertex non-manifold?

Returns:

1 if succesful, a negative value if the ball cannot be computed: -1 if a surface ball had too many elements, -2 if there are more than two references around, -3 if an edge cannot be found, and -4 if a volume ball had too many elements. Among these, -1, -3 and -4 can be taken as a sign that further remeshing is not possible, while -2 just mean the job could not be done.

Once these information have been listed, checks must then be made in order to ensure that the attempted collapse leads to a valid configuration.

For a standard internal edge, validity of the collapse is checked by:

int MMG5_chkcol_int(MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t iface, int8_t iedg, int64_t *list, int ilist, int8_t typchk)

Check whether collapse ip -> iq could be performed, ip internal ; ‘mechanical’ tests (positive jacobian) are not performed here

For a boundary edge, checks are performed thanks to function

int MMG5_chkcol_bdy(MMG5_pMesh mesh, MMG5_pSol met, MMG5_int k, int8_t iface, int8_t iedg, int64_t *listv, int ilistv, MMG5_int *lists, int ilists, MMG5_int refmin, MMG5_int refplus, int8_t typchk, int isnm, int8_t isnmint)

Check whether collapse point ip over iq could be performed, where ip is a boundary point.

‘Mechanical’ tests (positive jacobian) are not performed here.

If isnm is 1, the collapse occurs along an external MG_NOM edge.

If isnmint is 1, ip is an internal non manifold point and does not have normals. In this last case, lists, ilists refmin, refplus and isnm variables aren’t used (we neither have a surfacic ball nor “positive” and “negative” volumes)

Remark

edge lengths are not checked.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• k – index of element from which collapse occurs.

• iface – face through which collapse is performed.

• iedg – edge to collapse (in local face num).

• listv – pointer to the list of tetra in ball of p0.

• ilistv – number of tetra in ball of p0.

• lists – pointer to surfacic ball of p0.

• ilists – number of tetra in surfacic ball of p0.

• refmin – reference of one of the two subdomains in presence.

• refplus – reference of the other subdomain in presence.

• typchk – typchk type of checking permformed for edge length (hmax or MMG3D_LLONG criterion).

• isnm – 1 if edge is non-manifold.

• isnmint – 1 if ip is an internal non manifold point.

Returns:

ilistv if success, 0 if the point cannot be collapsed, -1 if fail.

This function starts by reordering the surface ball \(\texttt{lists}\) via the call of:

int MMG5_startedgsurfball(MMG5_pMesh mesh, MMG5_int nump, MMG5_int numq, MMG5_int *list, int ilist)

Reorder surfacic ball of point ip, so that its first element has edge (p,q) as edge MMG5_iprv2[ip] of face iface.

Parameters:

• mesh – pointer to mesh structure.

• nump – point to collapse (global num).

• numq – point receiving collapse (global num).

• list – pointer to surfacic ball of nump.

• ilist – number of elements in surfacic ball.

Returns:

2 if ball reordered, 1 otherwise.

in such a way that the first element \(\texttt{l=0}\) and last element \(\texttt{l=ilists-1}\) contain the collapsed edge \(\texttt{nump}-\texttt{numq}\) (and are thus those surface triangles vanishing in the process).

Then, \(\texttt{MMG5_chkcol_bdy}\) performs the following verifications:

• For all the tetras of the shell of the collapsed edge, it should not happen that either all four faces of the tetrahedron are boundary, or that the two identified faces via the collapse are boundary, as illustrated below:

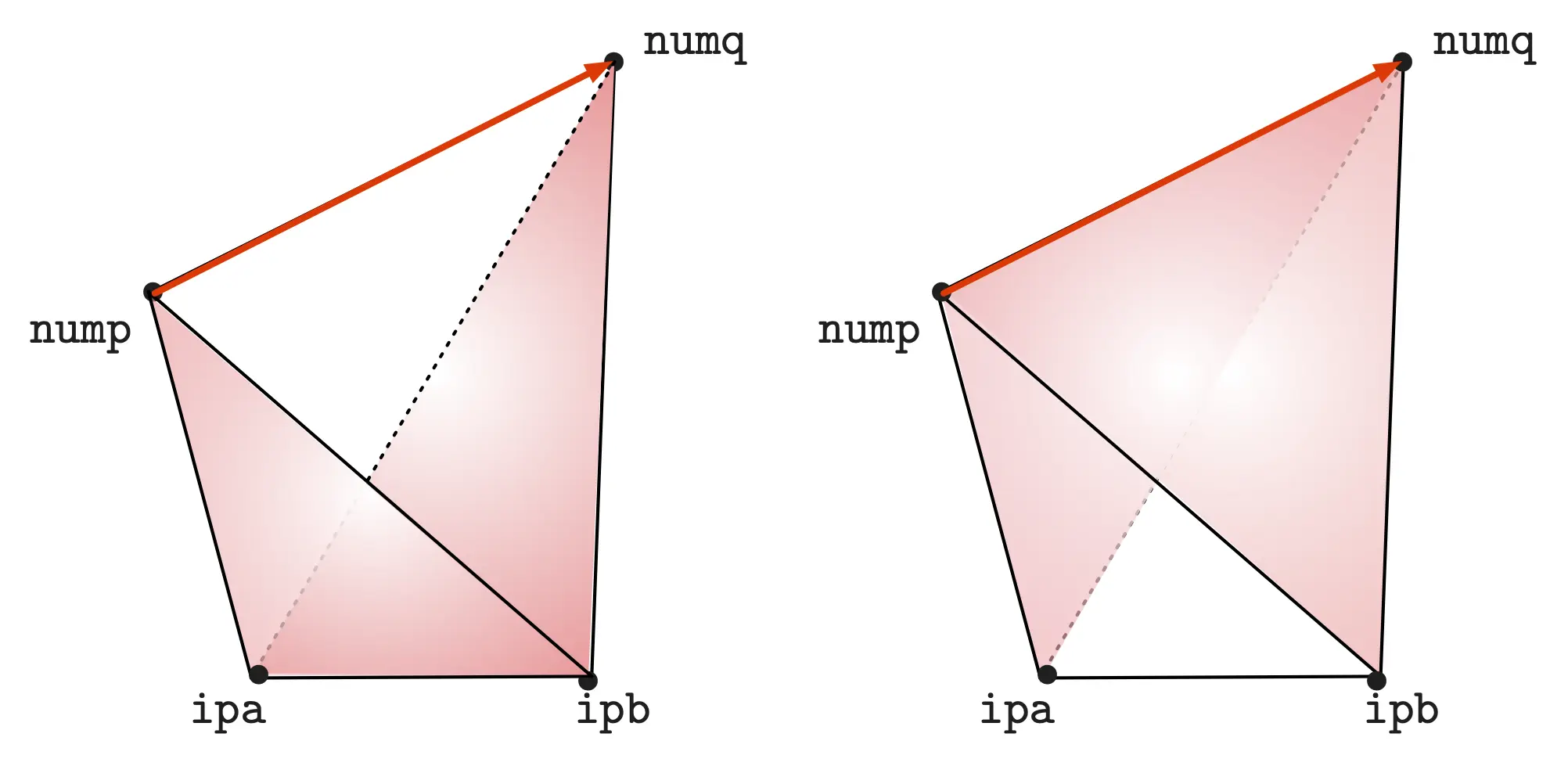
(Left) If the two merged faces in the shell tetrahedron \(\texttt{nump-numq-ipa-ipb}\) are boundary, collapse should be prevented; (right) If one of the two merged faces (in white) is not boundary, this phenomenon does not show up, even if the other three faces are boundary.

• Tetras in the ball of \(\texttt{p}\), outside the shell of \(\texttt{pq}\), are required not to get four boundary vertices as a result of the collapse;

• The Jacobian of the newly created elements stays positive (actually, the quality of the resulting elements is not too much degraded);

• Several tests are carried out concerning the surface ball of the collapsed point \(\texttt{p}\):

  • The angle between the normal vector to each face (but for the two disappearing) before collapse (\(\texttt{ncurold}\)) and after collapse (\(\texttt{ncurnew}\)) should be less than \(90^\circ\) (no flipping).

  • For each face \(\texttt{l=1,\cdots,ilists}\) in the surfacic ball, the deviation between the normal vector to the previous face \(l-1\) (\(\texttt{nprvold}\) or \(\texttt{nprvnew}\)) and that to \(l\) (\(\texttt{ncurold}\) or \(\texttt{ncurnew}\)) should not be increased too much.

  • The updated triangles \(\texttt{l=1,\cdots,ilists-2}\) do not show a too large degradation of the geometric approximation of the support.

Aside from these checks, several additional verifications are conducted to deal with the surface triangles gathered in the list \(\texttt{lists}\). Note that these are only external surface triangles (so that the degradation over the geometric approximation of the implicit boundary joining at the collapsed edge is not monitored). If option \(\texttt{-ls}\) is used or if collapsed is non-manifold, the following function is called

int MMG3D_chkmanicoll(MMG5_pMesh mesh, MMG5_int k, int iface, int iedg, MMG5_int ndepmin, MMG5_int ndepplus, MMG5_int refmin, MMG5_int refplus, int8_t isminp, int8_t isplp)

Check whether collapse of point np to nq does not create a non manifold situation at nq ndepmin, ndepplus = tetra of ref minus, plus in ball of np, not in shell of (np,nq).

Parameters:

• mesh – pointer to the mesh structure.

• k – index of element in which we collapse.

• iface – face through wich we perform the collapse

• iedg – edge to collapse

• ndepmin – index of an elt with ref refmin and outside the shell of edge.

• ndepplus – ndex of an elt with ref refplus and outside the shell of edge.

• refmin – reference of one of the two subdomains in presence

• refplus – reference of the other subdomain in presence

• isminp – 1 if we have found a tetra with ref refmin

• isplp – 1 if we have found a tetra with ref refplus

Returns:

0 if we create a non manifold situation, 1 otherwise

Otherwise, for a non-singular edge in standard adaptation mode, the following function is called:

static int MMG5_topchkcol_bdy(MMG5_pMesh mesh, MMG5_int k, int iface, int8_t iedg, MMG5_int *lists, int ilists)

Topological check on the surface ball of np and nq in collapsing np->nq ; iface = boundary face on which lie edge iedg - in local face num. (pq, or ia in local tet notation). See the Mmg Google Drive/Documentation/mmg3d/topchkcol_bdy3D.pdf for a picture of the configuration.

Parameters:

• mesh – pointer to the mesh structure.

• k – index of the starting tetra.

• iface – local index of the starting face in the tetra k.

• ideg – local index of the starting edge in the face iface.

• lists – surfacic ball of p.

• ilists – number of elements in the surfacic ball of p.

Returns:

0 if the check of the topology fails, 1 if success, -1 if the function fails.

Here,

• the collapse of the edge \(\texttt{iedg} = 0,1,2 \) on the face \(\texttt{iface}=0,1,2,3\) of tetra \(\texttt{k}\) is considered. More precisely, \(\texttt{nump}\) is collapsed on \(\texttt{numq}\) (see illustration below).

• The surfacic ball of \(\texttt{nump}\) is provided and it is assumed that the two vanishing faces in the collapse are \(\texttt{lists[0]}\) and \(\texttt{lists[ilists-1]}\) (typically, the function \(\texttt{MMG5_startedgsurfball}\) has been called previously).

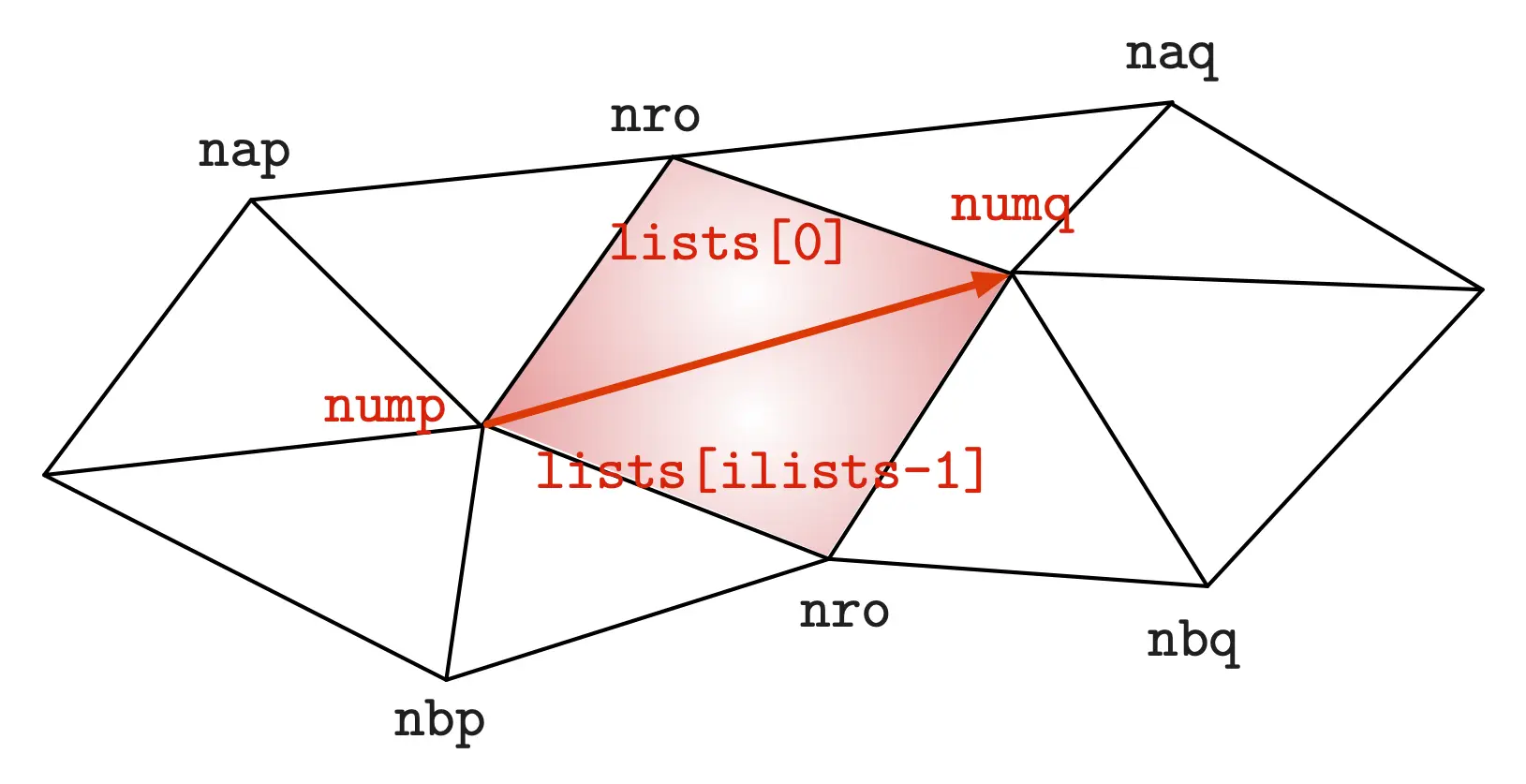
Configuration assumed by the function \(\texttt{MMG5_topchkcol_bdy}\).

This function then checks that:

• The points \(\texttt{nap}\) and \(\texttt{naq}\) are different, and that so are the points \(\texttt{nbp}\) and \(\texttt{nbq}\) (i.e. there is no small bubble of void).

• The deviation between the normal vectors of \(\texttt{nap-numq-nro}\) and \(\texttt{numq-naq-nro}\) is not much larger than that between \(\texttt{nump-numq-nro}\) and \(\texttt{numq-naq-nro}\) (and similarly for the configuration next to \(\texttt{lists[ilists-1]}\)).

If the configuration is valid, actual collapse is then performed by function:

MMG5_int MMG5_colver(MMG5_pMesh mesh, MMG5_pSol met, int64_t *list, int ilist, int8_t indq, int8_t typchk)

Collapse vertex p = list[0]%4 of tetra list[0]/4 over vertex indq of tetra list[0]/4. Only physical tests (positive jacobian) are done (i.e. approximation of the surface, etc… must be performed outside).

Parameters:

• mesh – pointer to the mesh

• met – pointer to the metric

• list – pointer to the ball of the point

• ilist – number of elements in the ball of the point

• indq – local index of the point on which we collapse

• typchk – type of check performed depending on the remeshing step

Returns:

np the index of the collpased point if success, 0 if we cannot collapse, -1 if we fail.

Edge swap

The third (and last step) of function \(\texttt{MMG5_anatet}\) consists in swapping faces.

Metric data

Second call to \(\texttt{MMG5_anatet}\)

Function MMG5_anatet is called again, with \(\texttt{typchk = 2}\).

Final adaptation phase

static int MMG5_adptet_delone(MMG5_pMesh mesh, MMG5_pSol met, MMG3D_pPROctree *PROctree, MMG5_int *permNodGlob)

Analyze tetrahedra and split long / collapse short, according to prescribed metric.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• PROctree – pointer to the PROctree structure.

• permNodGlob – if provided, store the global permutation of nodes

Returns:

0 if failed, 1 otherwise.

Vertex relocation

The vertex relocation procedure is called by \(\texttt{MMG5_adptet_delone}\). It is achieved by the function:

MMG5_int MMG5_movtet(MMG5_pMesh mesh, MMG5_pSol met, MMG3D_pPROctree PROctree, double clickSurf, double clickVol, int moveVol, int improveSurf, int improveVolSurf, int improveVol, int maxit, MMG5_int testmark)

Analyze tetrahedra and move points so as to make mesh more uniform.

Parameters:

• mesh – pointer to the mesh structure.

• met – pointer to the metric structure.

• PROctree – pointer to the PROctree structure.

• clickSurf – triangle quality threshold under which we want to move

• clickVol – tetra quality threshold under which we want to move

• moveVol – internal move

• improveSurf – forbid surface degradation during the move

• improveVolSurf – forbid volume degradation during the surfacic move

• improveVol – forbid volume degradation during the move

• maxit – maximum number of iteration

• testmark – all the tets with a mark less than testmark will not be treated.

Returns:

-1 if failed, number of moved points otherwise.

Essentially, this function travels all the vertices in \(\texttt{mesh}\) by travelling all the tetrahedra \((\texttt{k=1,...,mesh$\to$ne})\), all the faces (\(\texttt{i=0,...,3}\)), and the three vertices of each face \((\texttt{j=0,...,2})\) and calls a particular procedure depending on the geometric nature of the vertex (\(\texttt{MG_NOM}\), \(\texttt{MG_GEO}\), etc.).